Unit 3 - Electric Circuits
Resistors in Series v.s. Parallel
In series, the magnitudes of the resistors add up: $R_{eq} = \sum_{i=1}^{n} R_i$
However, in parallel, the inverse of the equivalent resistance is equal to the sum of the inverse of each resistor's magnitude: $\frac{1}{R_{eq}} = \sum_{i=1}^{n} \frac{1}{R_i}$
Resistivity
$R = \rho \, (\frac{L}{A})$
- $\rho$ is the resistivity, where the resistivity is a physical property of a resistory.
- A higher $\rho$ leads to a higher resistance, and vice versa.
Internal Resistance and Terminal Voltage
$V_{Terminal} = \varepsilon - Ir$
- For an imperfect battery, the emf $\varepsilon$ produced is not the experienced voltage within the circuit.
- Instead, the terminal voltage (the voltage experienced by the circuit) is the difference between the emf $\varepsilon$ of the battery and the voltage drop caused by the battery's internal resistance $Ir$.
Energy and Power
$P = IV = I^2 R = \frac{V^2}{R}$
$P = \frac{dE}{dt} \rightarrow E = \int P \, dt$
- Only the first form of the equation is given, but using Ohm's Law ($V = IR$), any of the 3 equations can be found.
RC Circuits
Charging
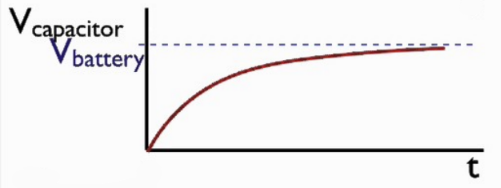
$V_C = V_0 \, (1-e^{\frac{-t}{RC}})$
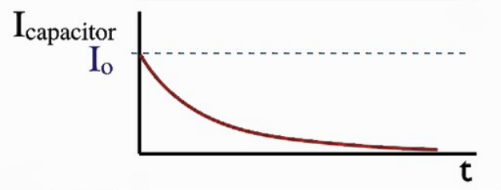
$I_C = I_0 \, (e^{\frac{-1}{RC}})$
Discharging
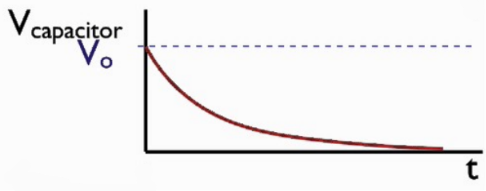
$V_C = V_0 \, (e^{\frac{-t}{RC}})$
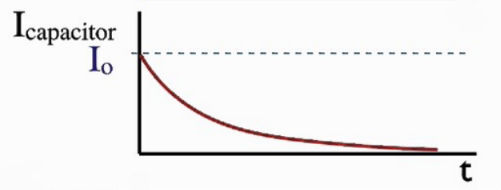
$I_C = I_0 \, (e^{\frac{-1}{RC}})$



